超临界转速运转

前面导出临界转数公式时，曾设摩擦力与钢球重量的切向分力相等，钢球没有滑动。在采用不平滑衬板和装球率占40~50%时，这种假设是符合实际的。倘若采用摩擦系数小的平滑衬板，又减少装球量使正压力降低，那么，摩擦力就小到不足以平衡球荷的切向分力，钢球于是有了滑动。

在这种情况下，尽管磨机的转速超过用公式（2-3）算得的nc好几倍，因为钢球有剧烈的滑下运动，它还是不会离心化。这就是磨机超临界转速运转的实质和必要的条件。R.T. 胡基在六十年代的研究指出，在适当的条件下，磨机的转速超过n_c值的20倍，钢球还不会离心化，仍然有磨矿效果。

超临界转速运转不仅在理论上突破了公式（2-5）的局限性，而且可以提高磨机的处理能力。生产实践指出，如果应用恰当，超临界转速运转可以提高磨机的生产力，虽然功率耗相应地增加，但比功率耗（即千瓦·时/吨）常常是降低的，如下表中的例子。磨机的转速和装球量是影响磨机生产率的两个关键性的因素。超过n_c值运转固然可以提高磨机生产率，但要求减少装球量，而减少装球量又会使生产率降低。所以不能片面地采用大幅度提高转速及大幅度减少装球量的办法，这反而会使生产率下降，如下图3-2-6反映的情况。当装球率减少到25%以下，即使将转速率提高到145%，生产率也达不到装球率为35~40%,(转速率为110~120%的。并且转速太高，磨机振动很厉害，也会造成危险。

要把磨机的转速提高到超过临界值，必须考虑原用的电动机的功率是否充足，传动部件的强度是不是够。磨机转速提高后，生产率加大，和磨机构成闭路的分级机的负荷也增加，必须采取措施提高分级机的生产能力和效率，要不然由于分级机的限制，效果未必好。超临界转速后，钢球与衬板之间和钢球与钢球之间有强烈的相对运动，磨损很厉害。为了解决这个问题，有用合金钢制衬板和钢球的，也有采用矿石自衬自磨的。试验研究和生产实践都指出：用普通磨机在超临界转速下进行矿石自磨，它的生产率可以达到在n_c以内用钢球磨矿的。衬板为特殊形状，由矿石自己去填补成一层壳，以便节约钢材。

由公式（2-7）可以得到

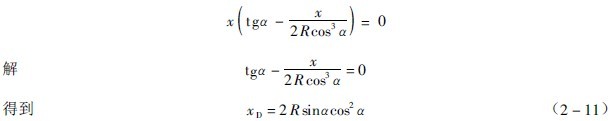
确定B点的坐标：B点是钢球抛落的终点，也是它开始圆运动之点，所以它的坐标x_b和y_b即公式（2-6）和（2-7）联立时的公解。将公式（2-7）中的y代入公式（2-6）中，然后逐步化简，得到

中，它的三个根x₁=x₂=x₃=0，即两轨这相交的坐标原点A 。在

中，第四个根即落回点B的x坐标，即

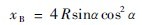
将x_b的值代入公式（2-7），求得

将公式（2-12）和（2-11）比较，可以看出

将公式（2-12）及（2-13）和公式（2-8）及（2-9）比较，可以看出

在已知脱离角a的情况下，可以根据以上各式算出各特殊点的坐标，坐作抛物落下运动时的抛物线即能准确地画出。如果要用到以O为原点的XOY系来表示落回点B的坐标，根据移轴规则（新坐标等于旧坐标减新原点的旧坐标），将公式（2-12）和（2-13）改写成

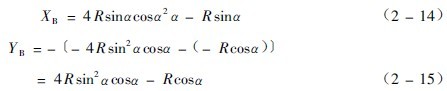
而落回角（、钢球中心与磨机中心的连线和X轴的夹角）可以求出为

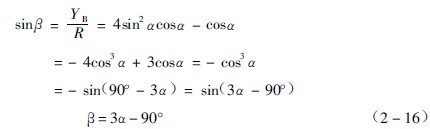
有的研究者如高伍（Gow）认为，每一个球到达脱离点之前，都受到它后面的球上升时的推力。因此上升得较脱离点高，抛物落下也较戴维斯理论算出的远。虽高伍根据这种方法提出了另外的计算公式，但尚未获公认，而戴维斯理论与实际资料仍然大致符合。