作用于钢球的力和钢球的运动状态

球磨和棒磨，都是由筒体转动使内部装的磨矿介质发生运动，因此对矿石产生磨碎作用。它们内部装的磨矿介质的运动，有很多相似之处，钢球的运动状态已经研究得比较充分，所以选它作为代表来作说明。既然磨矿作用是钢球运动产生的效果，所以研究钢球的运动学的目的，就在于对磨机的生产率，消耗的动力和合理的主要磨矿条件等作根本性的探讨。研究磨机内的钢球运动拍摄的照片，可以归纳为下图中的三种典型状态：泻落式、抛落式和离心运转。

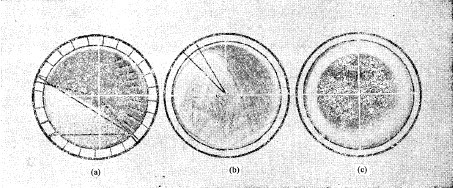
如果磨机的转速不高，全部球荷向上偏转一定角度，其中每个钢球都绕自己的轴线转动。当球荷的倾斜角超过钢球在球荷表面上的自然休止角时，钢球即沿此斜坡滚下。钢球的这种运动状态，叫做泻落，如图3-1-2中的（a）。在泻落式工作的磨机中，矿料在钢球间受到磨剥作用。如果磨机的转速足够高，钢球自转着随筒体内壁作圆曲线运动上升至一定高度，然后纷纷作抛物线下落。钢球落下的地方，叫底脚区，其中的钢球强烈地翻滚。这种运动状况，如图3-2-1中的（b），叫做抛落。在抛落式工作的磨机中，矿料在圆曲线运动区受到钢球的磨剥作用，在底脚区受到落下的钢球的冲击和强烈翻滚着的钢球的磨剥。倘若磨机的转速高到超过某一临界值，钢球就贴在衬板上不再落下。这种状态叫离心运转，知图3-2-1中的（c）。发生离心运转时，矿料也是贴着衬板的。以上这些情形，都是指磨机内装有一定数量的钢球说的。要是磨机内只有少量的球，它们只是在磨机内较低点摆动，并不发生上面讲的三种情况。用拍摄磨机内的介质的运动状态来研究它的运动规律，本世纪的二十年代已经开始，豪尔太恩、戴维斯、列文逊和我国的王仁东，都先后做过这方面的工作。钢球作泻落式运动的力学尚缺乏研究，以后只讲抛落式的。再详细地看看下面几张关于抛落式和离心运转的照片。

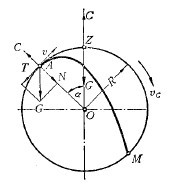
如下图，在球荷中任意取一钢球A₁，它处于球的重量G的作用下，并且有离心力C。G的切向分力使质点A₁沿切线方向运动；G的法向分力在第三和第五象限与离心力C的方向相同，在第二象限与C的方向相反。C与N的合力的反力，配合上与A₁接触处的摩擦系数（f），构成摩擦力F，它的方向与T力的相反，阻止T力沿切线方向运动。当钢球与筒壁没有相对运动的情况，T力和F力是相等的。钢球受力C和力N压着，与磨机成一整体，随磨机以同样的线速度v作圆曲线运动上升到A₃点。在此处，力C和力N的大小相等方向相反，F=0，切线分力T为后面的球上升时的推力所抵消。于是，钢球脱离筒壁，成为自由的，像与水平线成一角度并以速度v抛出物体那样，受自身重量的作用，作抛物线下落。

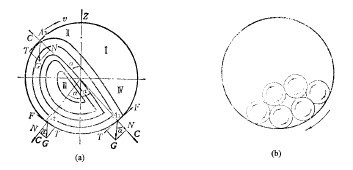
和离心力C相等，钢球即作抛物落下。如果磨机的速度增加，钢球开始抛落的点也就提高。到了磨机的转速增加到某一值v_c，离心力大于钢球的重量，钢球升到磨机顶点Z不再落下，发生了离心运转。由此可见，离心运转的临界条件是

多，可略而不计，R可以算是磨机的内半径，D就是它的内直径。由公式（2-3）可以看出，使钢球离心化所需的临界转数，决定于球心到磨帆中心的距离。外层球距磨机中心远，使它离心化所需的转数少；内层球距磨机中心近，使它离心化所需的转数也多。如果取磨机内半径用公式（2-3）算的结果作为磨机的转速，尽管外层球已经离心化了，但其他层球仍然能够抛落，还是可以磨细矿石。只有转数比用外层球按公式（2-3）求得的高出很多时，全部球层才会离心化，磨碎矿石的有用功才等于零。但是，装入的钢球希望全部能落下磨碎矿石，如果有一部分离心化，就会使有用功减少。因此，取磨机内半径用公式（2-3）算得的结果，说明要使外层球也不会离心化时磨机转速的限度，就没有必要去计算使其他层球离心化的磨机转数了。山此可见，磨机的临界转数，是使外层球也不会发生离心化的高转速（转/分）。尽管公式（2-3）是在没有考虑装球率及滑动等情况下导出的，但在采用不平滑衬板及装球率占40~50%时，它仍然符合实际情形。因此，生产中都采用公式（2-3）来计算磨机的临界转数，绝大多数磨机的转速都没有超过它。

即角a标志钢球开始抛落时已升到的位置，叫做脱离角。公式（2-5）指出，转速率愈高，脱离角愈小，钢球上升到的位置愈高。当脱离角为0^。时，转速率为1，即实际转速已等于临界转速，钢球到了磨机的顶点，要开始离心化了。