钢球直径的半理论公式推导——钢球直径的半理论公式与经验修正

公式（5-27）是粒度为d的矿块抵抗破坏的能量，公式（5-34）则是直径为D_b的钢球打击矿块时所具有的动能。从岩矿的破碎原理分析，当球的打击能量大于矿块抵抗破坏的能量时，即E_n≥E_抗时，矿块发生破碎，也即是：

对上式整理，找出目标函数Db（cm）与其它参数之间的数学关系为：

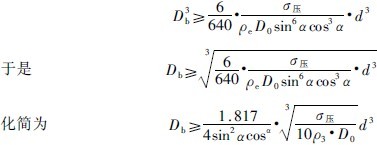
由钢球运动理论可知，若，式（5-35）经进一步简化，得：

公式（5-36）是钢球作抛落运动时导出的，球作泻落式运动时力学还无法计算。泻落式时球上升高度不高，用式（5-36）算出的结果还应适当加大。加之，前面推导公式时并未考虑钢球的切向速度V₁，的破碎作用。如果把V₁的作用考虑在内，上式计算的球径应考虑加大15%。这里按极限状态考虑，式（5-36）变为：

这个公式是在破碎力学原理的基础上用系统而严密的戴维斯和列文松钢球运动理

论推导出来的，它反映了钢球直径与磨机转速率钢球有效密度、磨机直径D（ D0与D直接有关、D0还与装球率有关）、岩矿抗$压极限强度压和给矿粒度d之间的关系。是目前所见球径公式中考虑因素较多的公式之一。从公式中可以看出，给矿粒度"大和岩矿抗压极限强度大时需要大的球径；磨机直径D小时也需要大的球径；钢球有效密度"!小时（即矿浆太浓，浮力过大，对球的缓冲作用大）也需要大的球径，故该公式反映了钢球破碎过程中的客观规律。而转速率对钢球直径的影响较复杂，难于直接看出，计算后才能看出。但当磨机转速率为100%时，公式算出Db——∞，表示此时钢球直径无意义，因为此时球已离心化而无破碎作用存在了。

此公式的结构框架是直接由理论推导出来的，但其中包括岩矿的抗压极限强度p_压，e_压不能由理论计算出来，只能借助实际工程测量得到，而且，在考虑泻落式运动时球径已作了经验性放大，因此，此公式只能算为半理论公式。此公式若要实际运用，还应对推导未考虑或假定中不符合实际的地方进行一些修正。

公式（5-37）在推导中抓住了几个主要因素，但也有一些因素未考虑。另外，为了推导公式方便而假定岩矿的力学性质是均匀的，但实际上岩矿的力学性质极不均匀。而且这些因素对球径的影响是很大的，只是它们难于定量地进入公式。如不考虑这些因素的影响，公式（5-37）也将产生大的误差，甚至使公式无使用价值。事实上，以前各国学者提出的各个球径公式中也均带有经验修正系数。对于这类复杂的工程技术问题，不经过经验修正的纯理论公式是没有实用价值的，因为简单的数学式子不可能把磨矿过程的影响因素都包括进去的。

现对公式（5-37）进行如下三个方面的修正：

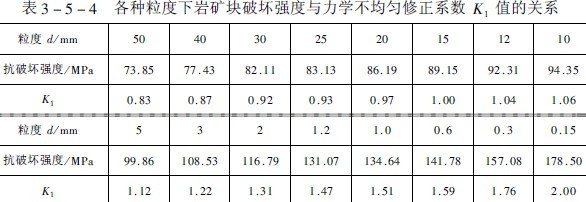
（1）岩石力学性质的不均匀性修正。粗矿块内部宏观和微观裂纹多，故强度低。而当矿块变细后各种裂纹逐渐消失，强度逐渐增大。原苏联学者曾对不同粒度的矿块作过破坏强度测定研究，测定资料见表（3-5-3）。但当矿粒度小于1mm时尚未见到测定资料。芬兰胡基教授曾作过不同粒度下的磨碎功耗测定，结果说明粒度变细与功耗的增加不是直线的比例关系。而呈类似幂函数的曲线关系增长，表明细磨时功耗增加比粒度变小快得多。参照胡基的研究和笔者进行的细磨研究，在表3-5-4, 中补充了1mm以下的破坏力数值和修正系数。

国外学者从F.C.榜德理论推导出球磨机的给矿粒度为1/2in（即12.7mm）时碎磨的能耗低。按欧美技术习惯，80% 过筛粒度为12.7mm时，相当于95% 过筛粒度的15mm。由于公式推导是在理想情况下进行的，可以认为求出合理的球径是在能耗低的情况下得到的。故以15mm为基准，小于15mm时矿块力学强度增大，大于15mm时矿块力学强度降低。若以K₁表示岩矿力学性质不均匀的修正系数，并以15mm为基准，定为1，则粒度大于15mm者K₁小于1，小于15mm者K₁大于1，按各粒级破坏力计算出K₁分别列入表3-5-4中。

（2）磨矿过程有效控制修正。磨矿过程中，粗磨和细磨的情况差异较大。粗磨时钢球既容易打着矿粒，球荷之间也容易啮住矿粒进行研磨，故磨碎的概率高，磨矿作用效率高，能量浪费小，即磨矿过程易于有效控制。细磨过程却不然，钢球打击矿粒和球荷间啮住矿粒均比较困难，磨碎的概率低，磨矿过程不太好控制，磨碎作用效率低，能量浪费大。
仍以能量消耗低的15mm为基准，并以K₂表示磨矿过程控制修正系数，大于15mm者K₂<1，小于15mm者K₂>1。由于目前还无法在此方面提出定量的修正依据，只有假设K₂的影响与K₁等同。

（3）矿浆粘度等因素的影响修正。粗磨时一定的矿浆粘度对磨矿是有利的，矿粒易粘附在钢球和衬板上形成一层矿粒层，当钢球与钢球或与衬板相碰撞时就能首先破碎矿粒，磨碎过程有效，能耗也就较低。细磨时粘度大则会产生有害影响，使能耗增大。如以K₃表示这方面的影响修正，但目前也难提出定量修正依据，仍仿K₂的处理办法，假定同一粒度下K₃的影响同K₁。

于是，设综合经验修正系数为K_c，按前面的假设得：

 K₂和K₃的假设是否合理，应以结果是否符合实际来进行检验。

 这样，球径半理论公式经修正后D_b（cm）成为：

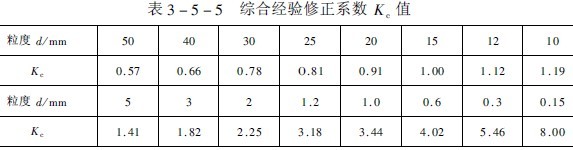
 公式（5-39）即为推导出的球径半理论公式。式中的综合修正系数K_c可按表3-5-5中数据选取。

 这样，在实际给定的磨机工作条件下就可以按公式（5-39）计算所需要的钢球直径。公式计算时采用cm.g.s制量纲。